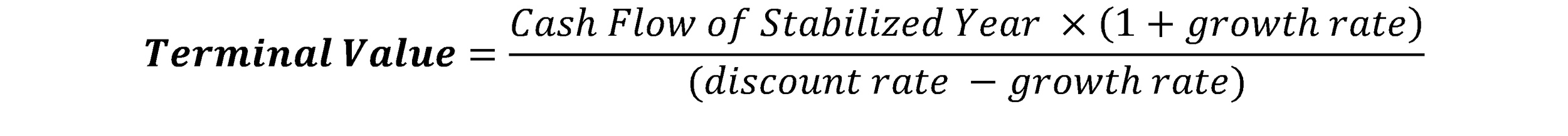Terminal Value (TV)
If you are reading this session, it should mean you should already know how to compute discount rate, present value and net present value. And if so, congratulations. You now know 90% of the process to evaluate a business or a project. Um….to be more precise, to evaluate them in “monetary value”.
In this section, let me introduce you to the remaining 10% of the evaluating process. It is called Terminal Value, or TV.
What the terminal value means is this:
“Terminal Value is the sum of the present value of cash flow at a certain point that goes…forever”
(I will explain the highlighted part later)
In the previous net present value session, I mentioned that “you can use NPV calculation to derive the present value of cash flow regardless of the time duration”. Even if you had cash flow that runs for 5 years or 10 years, or even 20 years, you always can calculate NPV by discounting the cash flow of each year and sum them.
Then you might wonder “does that mean…when I do a NPV calculation, I need to know when the cash flow ends? What if I am trying to evaluate a cash flow of a company that I believe is going to run like….forever…?”
The answer is simple. You create a cash flow from Year 0 (today) to Year Forever and discount them and add them all. Easy. Done.
Well…..you can’t do that, can you? To be precise, you might be able to do that, but that’s simply not practical. So, this is where the terminal value can help you. It calculates “the present value of the cash flow starting from a certain point in the future that goes forever”. And in finance, this “goes forever” is known as “perpetuity”.
Before looking into the detail, let me raise you 2 caveats:
First. The terminal value assumes that the cash flow beyond a certain point will follow the same trend. In other words, the terminal value can work only when the cash flow is “stabilized”, or in finance we say “under a steady state”. If you believe the cash flow grows steadily by 5% annually, then the terminal value assumes that every year the cash flow grows by 5% forever. If you believe the cash flow growth fluctuates in the future, then you cannot use the terminal value. Well, you can use it, but the result will not reflect any potential fluctuation. If you believe you will steadily keep receiving the same amount of cash every year, then you can use the terminal value. But if you believe that you will get random amount of cash throughout the years to follow, then you cannot use the terminal value. Again, the terminal value calculation is only applicable when the cash flow is in a steady state (=stabilized).
Second (and this is the reason I highlighted one part in the quotation above). The terminal value is NOT necessarily the present value of Year 0. It usually is the present value looking from a certain point in the future. For example, if you believe a cash flow enters a steady state in Year 10 and goes perpetuity, then you calculate a terminal value of cash flow of a steady state that starts from Year 11 and beyond. But, this terminal value is NOT the present value of Year 0, but rather, it’s the “present value of cash flow from Year 11 and beyond, looking at Year 10”. Therefore, once you calculate the terminal value, make sure you don’t stop the work, yet. Because, you further need to discount the terminal value, which is Year 10 value, to the present value of Year 0. So, whenever you calculate a terminal value, its so important that you understand “at which year you are calculating the terminal value”, because you also need to discount that to the actual present value.
Let’s imagine this: Say there' is a business that’s generating cash flow. Upon a computation, you derived a discount rate of 5% (WACC). Up to Year 10, the cash flow isn’t steady because it’s rather a new business in the market, so is quite volatile. It generates a lot of cash in some years, but only a little in some years. However, upon further analysis, you could notice that the business will enter a steady state in Year 10 when it generates $200. From there, the business grows cash flow by 3% and for perpetuity. Now, you want to know the monetary value of the business. How do you do that?
Here’s the cash flow of this fictional business:
And these are the 4 steps you need to do.
Calculate the NPV of cash flow for the unstabilized years, which is Year 0 through Year 10.
Calculate the terminal value at Year 10 of the stabilized cash flow that runs Year 11 and beyond.
Further convert the terminal value (value of infinite from Year 10 perspective) to the present value.
Add (1) and (3).
I’m sure you know how to work on the (1). You discount cash flow of each year from Year 0 to Year 10 and add them, which will be $933.
Now. For (2), the calculation of terminal value, you will have to use a formula. But, none of the variables will be new to you:
So, this $10,300 is “the amount of all the cash flow from Year 11 to perpetuity, discounted to Year 10’s value” (if you don’t know what I mean, revisit the caveat I wrote above). Therefore, you still need to further discount this $10,300 to the present value, the value at Year 0. With the present value formula, you should get $6,323.
And, finally! You add the NPV of cash flow of the unstabilized year, or $933, and the NPV of the terminal value, or $6,323, to derive the NPV of the all cash flow; $7,256. Well done!
Now……
some of you may be wondering from the beginning “If the cash flow runs perpetuity, wouldn’t the sum of all the cash flow be so large that you can’t even…calculate? But why is the terminal value only $6,323 in this exercise, which is not that big…?” That’s a really good question. I had the same queries when I first studied finance.
A quick answer to your question will be “Yes, since the cash flow goes perpetuity, the number will keep adding up perpetuity. But, because of the discounting, the further you go along the time horizon, the smaller the numbers will be, so that any further additions beyond certain point will not going to affect the NPV of all cash flow much”. In other words, the terminal value says “this is good enough to indicate what the perpetuity will be”.
Here’s the proof.
First, let’s revisit what the terminal value means:
“Terminal Value is the sum of the present value of cash flow at a certain point that goes perpetuity”
So, in a sense, what the terminal value is doing is calculating the present value of each year and adding them up. In the example above, therefore, the terminal value is the sum of PV of cash flow on Year 11, PV of cash flow on Year 12, PV of cash flow on Year 13….and so on (be careful here that PV is the present value at Year 10, not Year 0). You can notice the present value calculation is involved, right?
Ok. Then, let’s have a look at the present value formula:
Because the cash flow is in a steady state, the numerator grows at a steady rate, which, in this exercise, is 3%. Putting it in a mathematical expression, the numerator grows by “(1+3%) ^ Year X”. By the same token, if you look at the denominator, you can tell it grows by “(1+5%)^ Year X”. So what’s happening is that if you line up all the present value formula for each future years, you can see that the denominator is growing at a higher rate than the numerator. See the graph below:
If you recall what you learned in the math class when you were in middle school, in fraction, the larger the denominator is compared to the numerator, the smaller the answer will be. And this is why we say “the present value will be smaller the more you go further along the time horizon”.
For those still not sure, you can try it out by actually drawing a cash flow that starts at $200 and grows by 3% for, say, 90 years. And keep the discount rate at 5%.
See? Although the denominator, the cash part, keeps getting larger and larger by 3%, the present value goes lower and lower, eventually reaching near $0. Again, this is because the denominator is growing at a higher rate than the numerator. And, because the present value becomes so small in the future, almost nearing $0, adding or missing any of the present value beyond certain point would not make any difference. Hence, taking everything into account, the terminal value tells you “well…for your cash flow, this is a good and enough estimate for the perpetuity”
I’m sensing some of you still wondering this “What do we do if the growth rate is larger than the discount rate?” The short answer to that is “such case is theoretically impossible”. Let me explain to you, why.
As explained in the discount rate chapter, the discount rate incorporates “what we think the risk and the expectation level should be based on all the factors like the market, the investors, the competitor, etc.” So, in finance, we consider discount rates are a good reflection of the entire economy. On the other hand, the growth rate is “how much a company can grow annually and (for terminal value calculation) perpetuity”. Hence, the growth rate is a good reflection of a company itself. So, if you think the growth rate is higher than the discount rate, you are implying that the company grows at a higher rate than the economy itself. Do you think that’s possible? A company is supposed to grow by enjoying some shares and resources of the economy (money, people, activities, competitors, etc.), so, theoretically, a company CANNOT grow faster than the economy because, if so, the company will eventually have nothing from the economy to enjoy, leading to…..no growth. I hope you got the idea.
(Think this way…if all the animals on the planet inhaled oxygen faster than it is produced…..what do you think will happen…?)
Congratulations. Now you have completed the terminal value session. With NPV, discount rate and the terminal value, you now know how to evaluate a monetary value of cash flow, hence you can evaluate anything that generates cash flow; business, project, peer-lending, loan, mortgage…you name it.
As I’ve been reiterating, many finance concepts seem very complicated and difficult. But, whenever you learn a new topic, I strongly recommend you to create an easy version of exercise and work on it. Once you work on it, then play around with it to see consequences. You can make 5 year cash flow and plug in random discount rates to see what the NPV will be. You can delay some cash receipts and see how the NPV is affected. You can also use some Excel functions like Goal-Seek to see what discount rate is required to achieve your expected NPV. Once you comprehend the concept, then you apply it to a real world scenario. Figures, digits, signs, terms might be different from what you’ve learnt, but, what you are doing don’t change.